Scientic / Milankovitch / Documentation / Les paramètres orbitaux de Milankovitch
Les paramètres orbitaux de Milankovitch
L’excentricité de l’orbite Terrestre
D’après la première loi de Kepler ou Loi des orbites, les planètes décrivent des orbites en forme d'ellipses dont le Soleil occupe un des foyers.
Une ellipse est une courbe plane fermée définie comme l'ensemble des points dont la somme des distances à deux points fixes, appelés foyers, est constante.
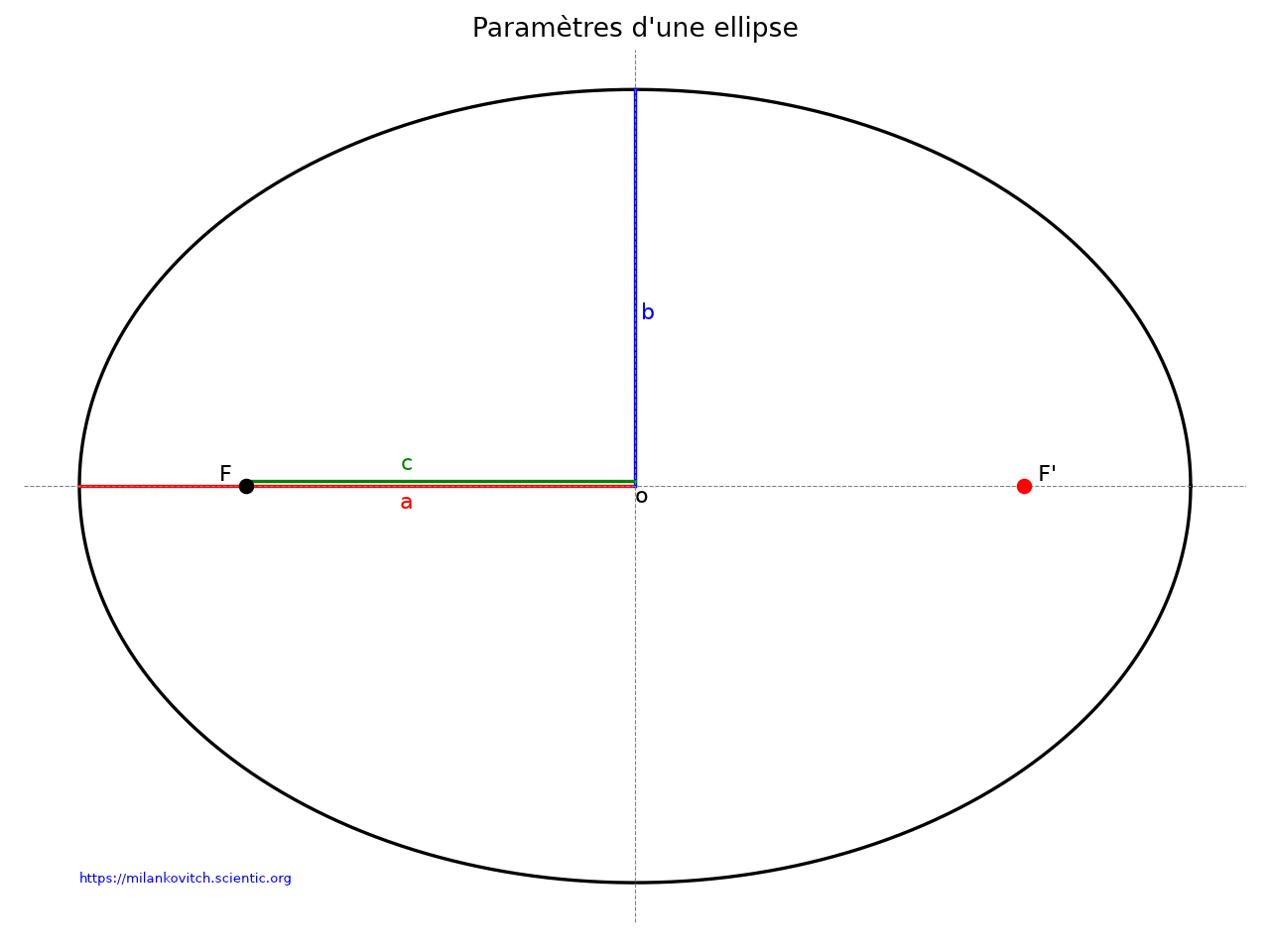 |
Paramètres de l’ellipse
Le demi-grand axe a représente la moitié de la longueur de l'axe principal de l'ellipse. L'axe principal est la plus grande distance entre deux points de l'ellipse.
Le demi-petit axe b représente la moitié de la longueur de l'axe secondaire de l'ellipse. L'axe secondaire est perpendiculaire à l'axe principal et correspond à la plus petite distance entre deux points de l'ellipse.
La demi-distance focale c représente la distance entre le centre de l'ellipse et l'un des deux foyers. Avec: c = (a2 - b2)1/2
|
Vu du pôle Nord céleste, la terre se déplace sur son orbite autour du soleil dans le sens prograde (sens direct ou sens anti-horaire)
L'excentricité caractérise la forme de l'ellipse. Elle est définie par la relation : e = c / a
L’excentricité est toujours comprise entre 0 et 1: 0 <= e <= 1
- Quand e = 0 : l'ellipse est un cercle parfait.
- Quand e est proche de 1 : l'ellipse est très allongée.
Les variations de l’excentricité
L’excentricité de l’orbite terrestre varie entre 0.000055 et 0,0679. Elle est actuellement de 0,01671022
L’analyse spectrale met en évidence une double périodicité:
- Une péridoicité de 100 000 ans. (Fréquence de 10 µHz soit 10 x 10-6 cycles / an)
- Une périodicité de 400 000 ans. (Fréquence de 2.5 µHz soit 2.5 x 10-6 cycles / an)
C’est davantage visible sur l’analyse spectrale par transformation de Fourier.
Les conséquences climatiques des variations de l’excentricité
Conséquences climatiques des variations de l’excentricitéLa variation de chaque paramètre est considérée indépendamment des autres paramètres dont les valeurs sont considérées similaires aux valeurs actuelles
|
Situation minimale |
Situation actuelle |
Situation maximale |
| Excentricité |
0.0000550 |
0,01671022 |
0,0679000 |
| Distance au Soleil lors du solstice d'été |
149 608 019 km |
152 034 266 km |
159 462 982 km |
| Distance au Soleil lors du solstice d'hiver |
149 591 981 km |
147 161 545 km |
139 667 574 km |
| Variation annuelle de distance |
0,01 % |
3,2 % |
12,41 % |
| Energie reçue lors du solstice d'été |
343.09 w/m2 |
332.23 w/m2 |
301.99 w/m2 |
| Enregie reçue lors du solstice d'hiver |
343.16 w/m2 |
354.59 w/m2 |
393.66 w/m2 |
| Variation annuelle d’énergie reçue |
0,02 % |
4,96 % |
23,28 % |
Les variations de l’excentricité font varier les distances Terre - Soleil au cours de l’année ce qui induit des variations de l’énergie solaire reçue au cours de l’année.
Dans la situation minimale, on a globalement moins de contrastes énergétiques au cours d’une année par rapport à la situation actuelle. Cependant si on envisage la comparaison par rapport à la situation actuelle, en termes de contrastes saisonniers en fonction des hémisphères, et en considérant une précession et une obliquité similaires à la situation actuelle:
- Dans l’hémisphère Nord, les étés sont plus chauds et les hivers plus froids. Il y’a donc davantage de contrastes saisonniers dans l’hémisphère Nord.
- Dans l’hémisphère Sud, les hivers sont moins froids et les étés sont moins chauds. Il y’a donc moins de contrastes saisonniers dans l’hémisphère Sud.
Dans la situation maximale, on a globalement plus de contrastes énergétiques au cours d’une année par rapport à la situation actuelle. Cependant si on envisage la comparaison par rapport à la situation actuelle, en termes de contrastes saisonniers en fonction des hémisphères et en considérant une précession et une obliquité similaires à la situation actuelle:
- Dans l’hémisphère Nord, les étés sont moins chauds et les hivers moins froids. Il y’a donc moins de contrastes saisonniers dans l’hémisphère Nord.
- Dans l’hémisphère Sud, les hivers sont plus froids et les étés sont plus chauds. Il y’a donc davantage de contrastes saisonniers dans l’hémisphère Sud.
L’obliquité
L’obliquité (ou inclinaison de l’axe de rotation sidérale de la terre) est défini par l’angle entre l’axe de rotation sidérale de la Terre et la normale à l’écliptique (perpendiculaire au plan de l’écliptique défini par la rotation de la Terre autour du Soleil).
Les variations de l’obliquité
L’obliquité est actuellement de 23°27' (soit 23,45°) , elle varie entre 21,9° et 24,5°.
L’analyse spectrale met en évidence une périodicité de 40 000 ans. (Fréquence de 25 µHz soit 25 x 10-6 cycles / an).
Les conséquences climatiques des variations de l’obliquité
Les variations de l’obliquité n’entraînent pas de variations globales de l’énergie solaire reçue par la terre, mais entraînent des variations spatiales et temporelles de la répartition de l’énergie reçue.
Les variations de l’obliquité font varier les angles d’incidences des rayons du Soleil en une latitude donnée au cours de l’année, ce qui induit des variations de l’énergie reçue en une latitude donnée au cours de l’année.
| Situation minimale |
Situation actuelle |
Situation maximale |
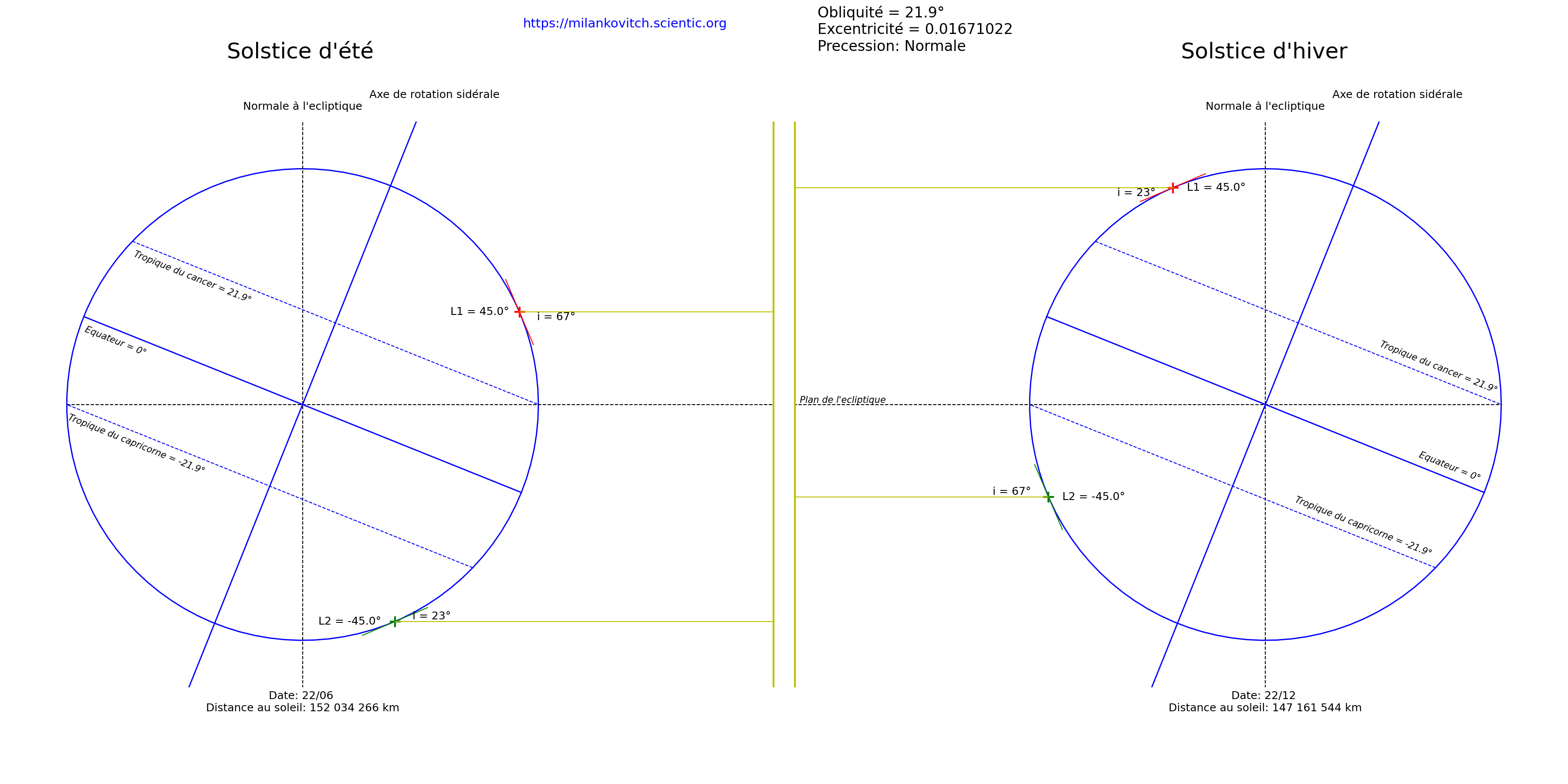
| Obliquité = 21,9° |
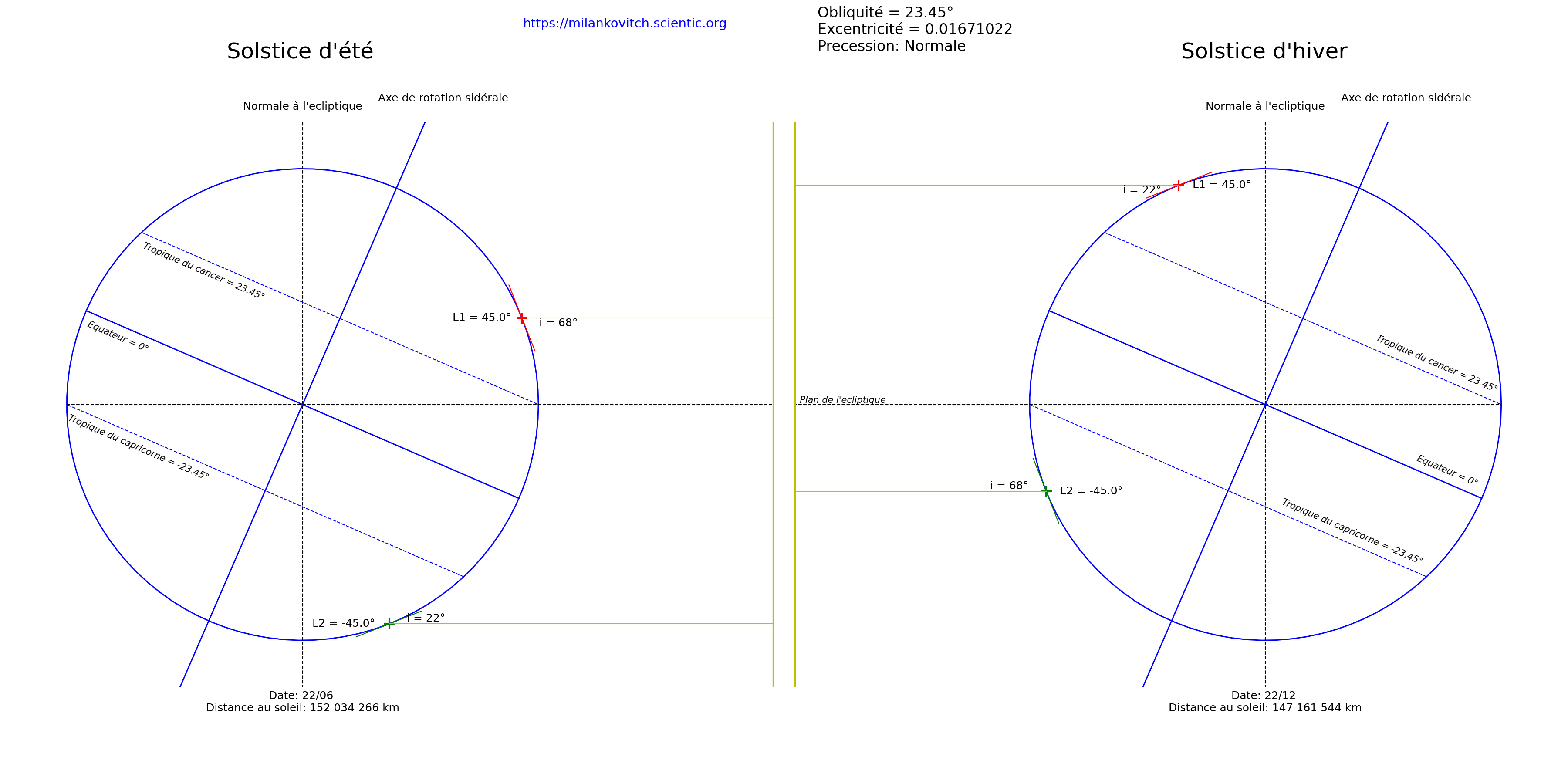
Obliquité = 23,45° |
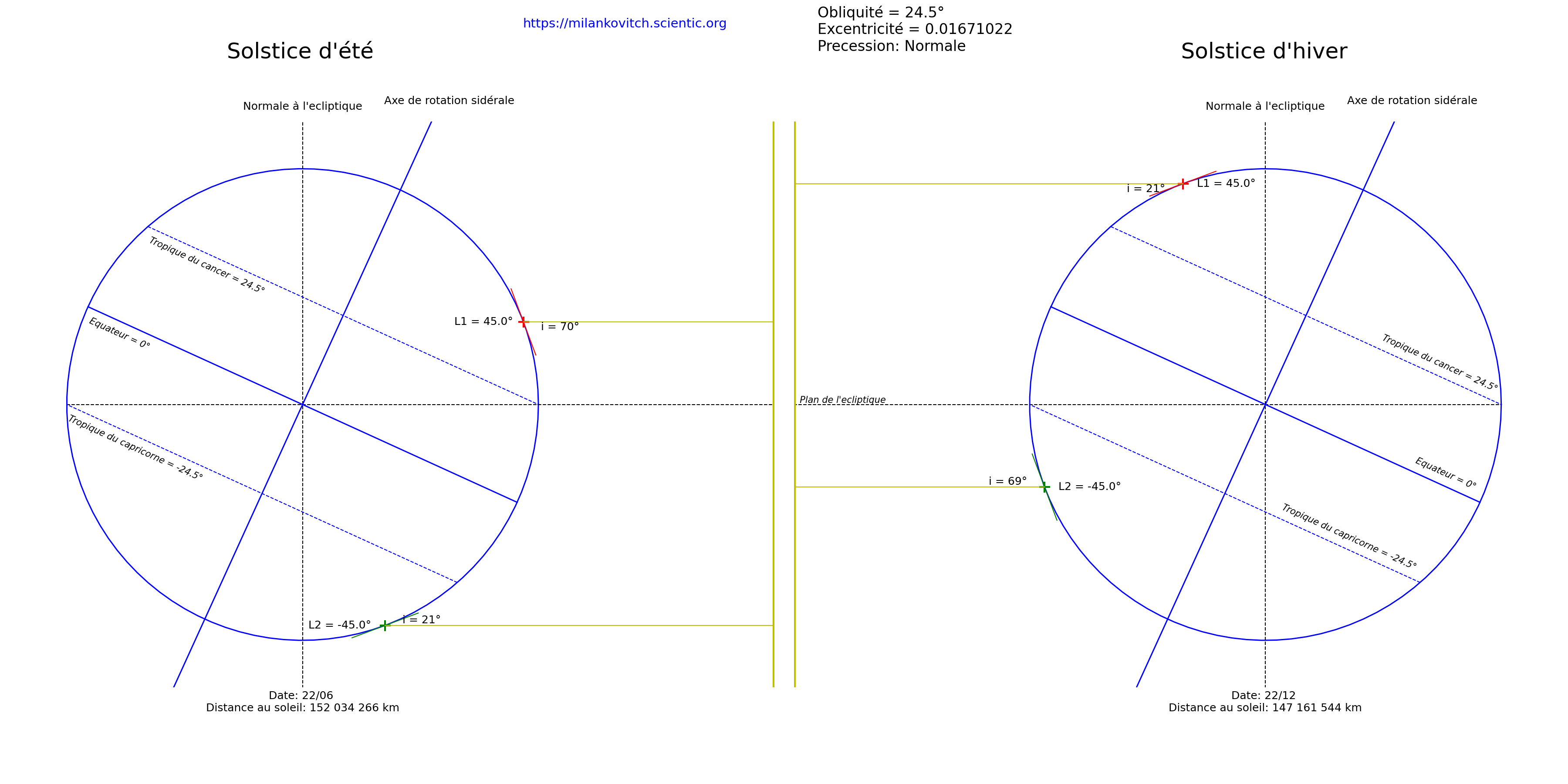
Obliquité = 24,5° |
 |
 |
 |
Plus l’angle d’incidence des rayons solaires est proche de 90°, plus l’énergie du rayon solaire se repartie sur une petite surface et plus l’énergie reçue à la surface de la terre (en w/m2) est forte.
Si l'obliquité diminue par rapport à la situation actuelle:
- L'angle d'incidence des rayons solaires augmente au solstice d'hiver (hiver moins froid) et diminue au solstice d'été (été moins chaud) dans l'hémisphère Nord. Il y'a moins de contrastes saisonniers.
- L'angle d'incidence des rayons diminue au solstice d'hiver (été moins chaud) et augmente au solstice d'été (hiver moins froid) dans l'hémisphère Sud. Il y'a moins de contrastes saisonniers.
Si l'obliquité augmente par rapport à la situation actuelle:
- L'angle d'incidence des rayons diminue au solstice d'hiver (hiver plus froid) et augmente au solstice d'été (été plus chaud) dans l'hémisphère Nord. Il y'a davantage de contrastes saisonniers.
- L'angle d'incidence des rayons augmente au solstice d'hiver (été plus chaud) et diminue au solstice d'été (hiver plus froid) dans l'hémisphère Sud. Il y'a davantage de contrastes saisonniers.
Les précessions
La longitude du périhélie (ϖ) est un angle qui mesure la position du périhélie (le point où la Terre est au plus proche du Soleil) par rapport à un référentiel fixe: la direction du point vernal: γ. Cet angle est mesuré dans le plan de l'écliptique à partir de la direction du point vernal (γ) jusqu'au périhélie, dans le sens prograde (sens direct ou sens anti-horaire). La direction du point vernal (γ) représente la direction dans laquelle est vu le Soleil depuis la Terre à l'équinoxe de printemps. La valeur actuelle (2025) de la longitude du périhélie est de 102,937°
La longitude du périhélie est en fait la somme de deux angles mesurés dans deux plans différents : ϖ = Ω + ω
- La longitude du nœud ascendant (Ω) : C'est l'angle mesuré dans le plan de référence (P2). Il est mesuré depuis la direction du point vernal (γ) jusqu'au nœud ascendant (☊) de l'orbite (le point où le plan orbital (P1) de la planète coupe le plan de référence (P2) en montant du sud vers le nord). Sa valeur actuelle (2025) est de −11,260°.
- L'argument du périhélie (ω) : C'est l'angle mesuré dans le plan de l'orbite de la planète (P1). Il est compté à partir du nœud ascendant (☊) jusqu'au périhélie (le point de l'orbite le plus proche du Soleil). Sa valeur actuelle (2025) est de 114,2°.
Diagramme des éléments orbitaux.Cette image est une version modifiée de Bahnelemente.svg (GFDL) par ArtMechanic.Cette image est sous la licence GNU Free Documentation License (GFDL).
Lorsqu’on étudie les cycles de Milankovitch, on se place dans un référentiel lié à la direction du point vernal et la longitude du périhélie varie alors au cours du temps du fait de la précession orbitale (qui fait varier la position du périhélie) et du fait de la précession axiale (qui fait varier la direction du point vernal)
Attention, la longitude du périhélie est un angle (ou plus exactement la somme de 2 angles), tandis que les précessions sont des variations de ces angles. Mais on utilise les mêmes symboles (ϖ , Ω , ω ) pour indiquer les valeurs de ces angles (en degrés ou radians) et pour indiquer leurs variations ou vitesses angulaires (en secondes d’arc / an).
La précession orbitale (ou précession du périhélie)
Les perturbations gravitationnelles des autres planètes, principalement Jupiter et Saturne font tourner l’ellipse entière (dans son propre plan) autour du soleil. Ainsi, dans un référentiel fixe (inertiel), cette précession orbitale fait varier lentement la position du périhélie et donc la longitude du périhélie.
Du fait de ce mouvement de l’ellipse, la longitude du noeud ascendant (Ω) diminue (sens rétrograde) d’environ –39,6″/an tandis que l’argument du périhélie (ω) augmente (sens prograde) d’environ +11,6″/an.
Donc la précession orbitale fait varier la longitude du périhélie (ϖ = Ω + ω) dans le sens rétrograde de −28″/an, avec une périodicité de 112 000 ans
Attention:
- Dans un référentiel lié à la diréction du point vernal (γ), le plan orbital de la Terre (et donc Ω) est considéré comme quasiment fixe par rapport au plan de référence. Donc ϖ ≈ ω. C’est pourquoi, dans les modèles climatiques, on assimile la variation de la longitude du périhélie à celle de ω uniquement.
- Dans un référentiel fixe (inertiel): ϖ = Ω + ω
La précession axiale (ou précession des équinoxes)
Les forces gravitationnelles du Soleil et de la Lune sur le renflement équatorial terrestre font vaciller l’axe de rotation sidérale de la terre comme une toupie autour de la normale à l’écliptique. Ainsi, dans un référentiel fixe (inertiel), cette précession des équinoxes fait reculer la direction du point vernal (γ) sur l’écliptique d’environ -50,3″/an (sens rétrograde) , avec une périodicité de 25 772 ans.
C’est ce mouvement qui fait que les étoiles changent lentement de coordonnées , et que les constellations "du zodiaque" associées aux saisons changent avec les millénaires. Depuis 2000 ans, la direction du point vernal pointe vers la constellation des Poissons mais elle est actuellement très proche d’entrer dans le Verseau.
Cette précession axiale est qualifiée de précession des équinoxes car en raison de ce mouvement, chaque année la date de l'équinoxe précède celle de l'année d’avant (d'environ 20 minutes).
Attention:
- Dans un référentiel lié à la direction du point vernal (γ), la précession axiale modifie la position du repère de référence (le point vernal γ), ce qui entraîne une variation apparente de Ω et donc de ϖ.
- Dans un référentiel fixe (inertiel) la précession axiale ne modifie pas la géométrie réelle de l’orbite ni les valeurs de Ω et ω.
La précession climatique
C’est la variation apparente de la position du périhélie par rapport à la direction du point vernal (γ) qui résulte de la combinaison du mouvement du point vernal γ (précession axiale), et du mouvement du périhélie ϖ ≈ ω (précession orbitale) lorsqu’on se situe dans un référentiel lié à la direction du point vernal (γ).
Cette variation relative entre la direction du point vernal γ et le périhélie engendre la précession climatique (ou précession des saisons), qui a une périodicité de 23 000 ans.
En cinématique céleste:
Précession climatique = Précession orbitale (ϖ) - Précession axiale (γ) = 11,6″/an - (-50,3″/an) = +61,9″/an (prograde).
Cette formule donne une vitesse angulaire de +61,9″/an soit +0,017194°/an soit environ +17° pour 1000 ans. C’est la variation que l’on retrouve dans les données de Laskar. Cette variation annuelle traduit une périodicité T = 360° / 0,017194 ≈ 20 936 ans. En raison d’autres pérturbations (notamment la variation de l’excentricité) on retient une valeur de T ≈ 23 000 ans. (Fréquence de environ 43 µHz soit 43 x 10-6 cycles / an).
En climatologie orbitale:
Précession climatique = excentricité * sin(ϖ)
Cette formule donne une grandeur sans dimension, liée à l’intensité saisonnière de l’insolation.
Les conséquences climatiques de la précession
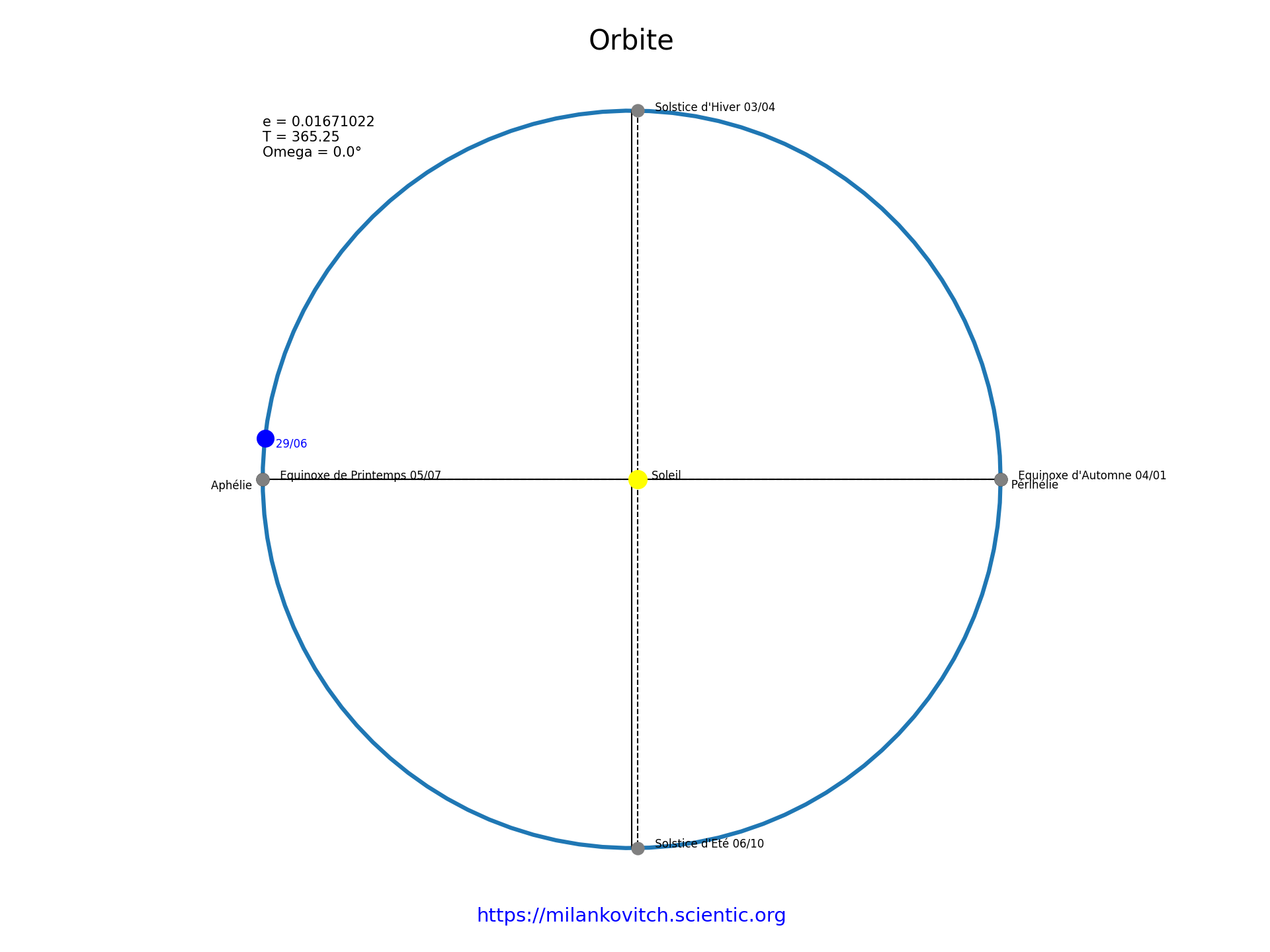
| ϖ = 0° |
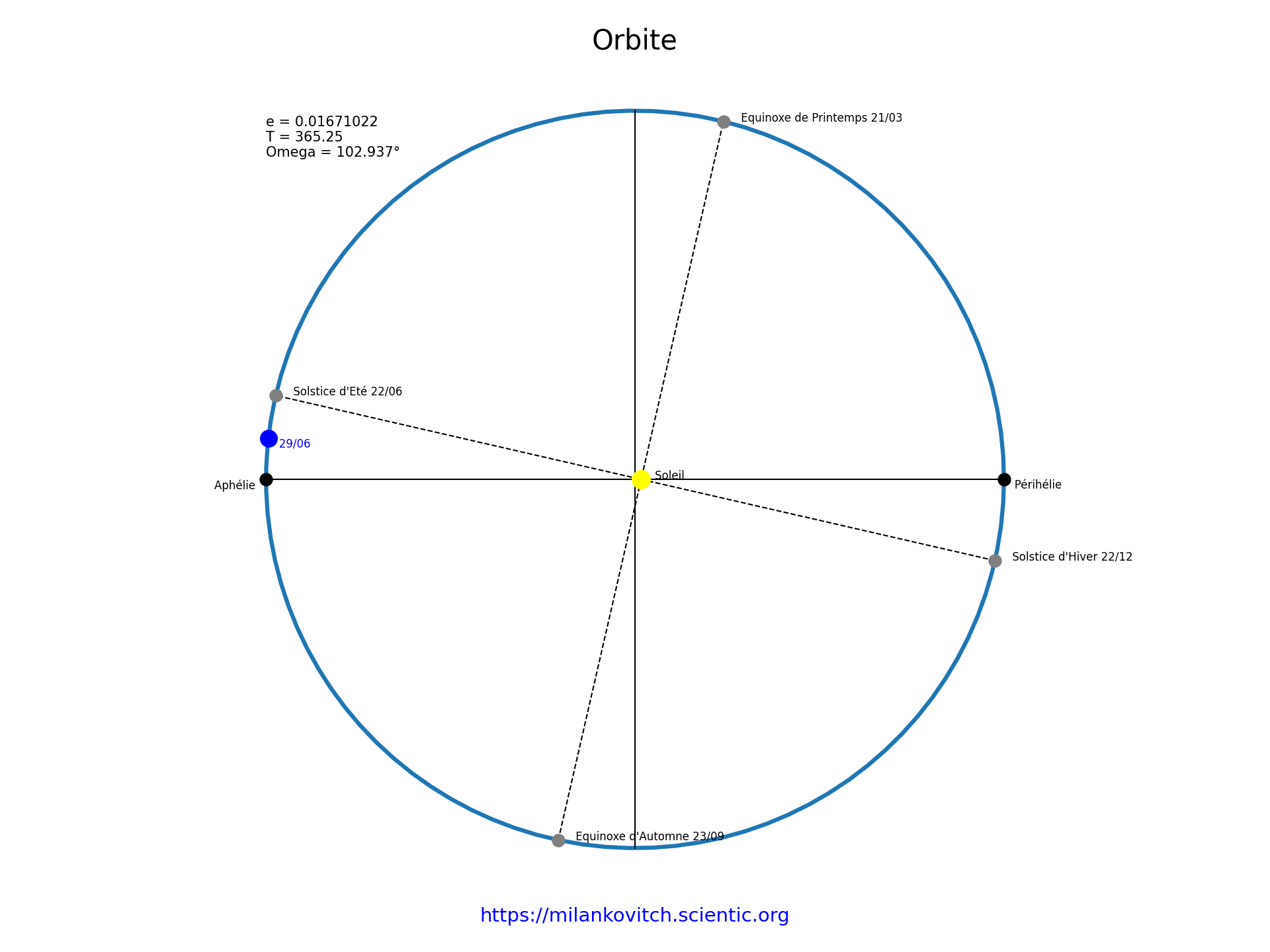
0° < ϖ < 180° |
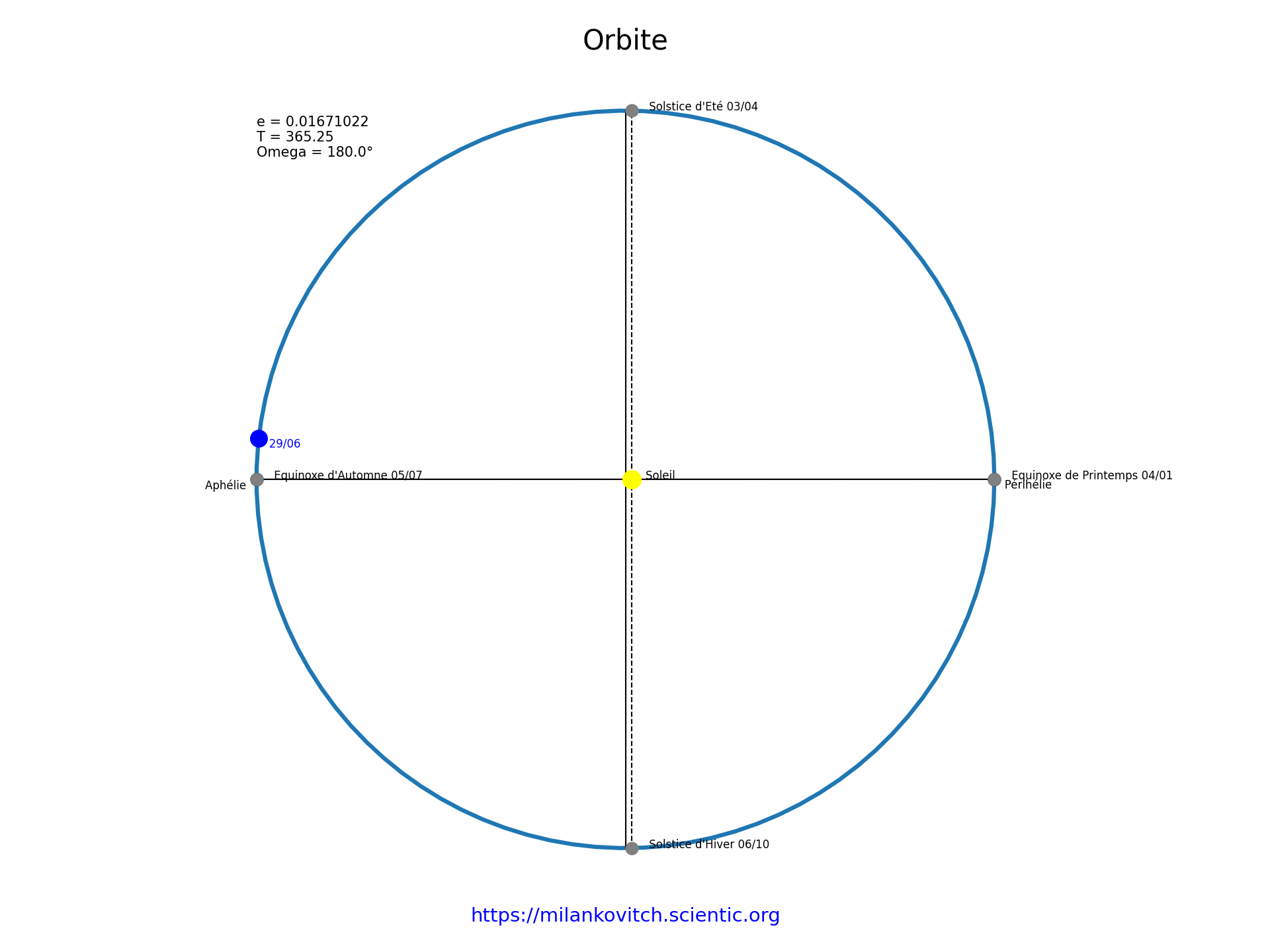
ϖ = 180° |
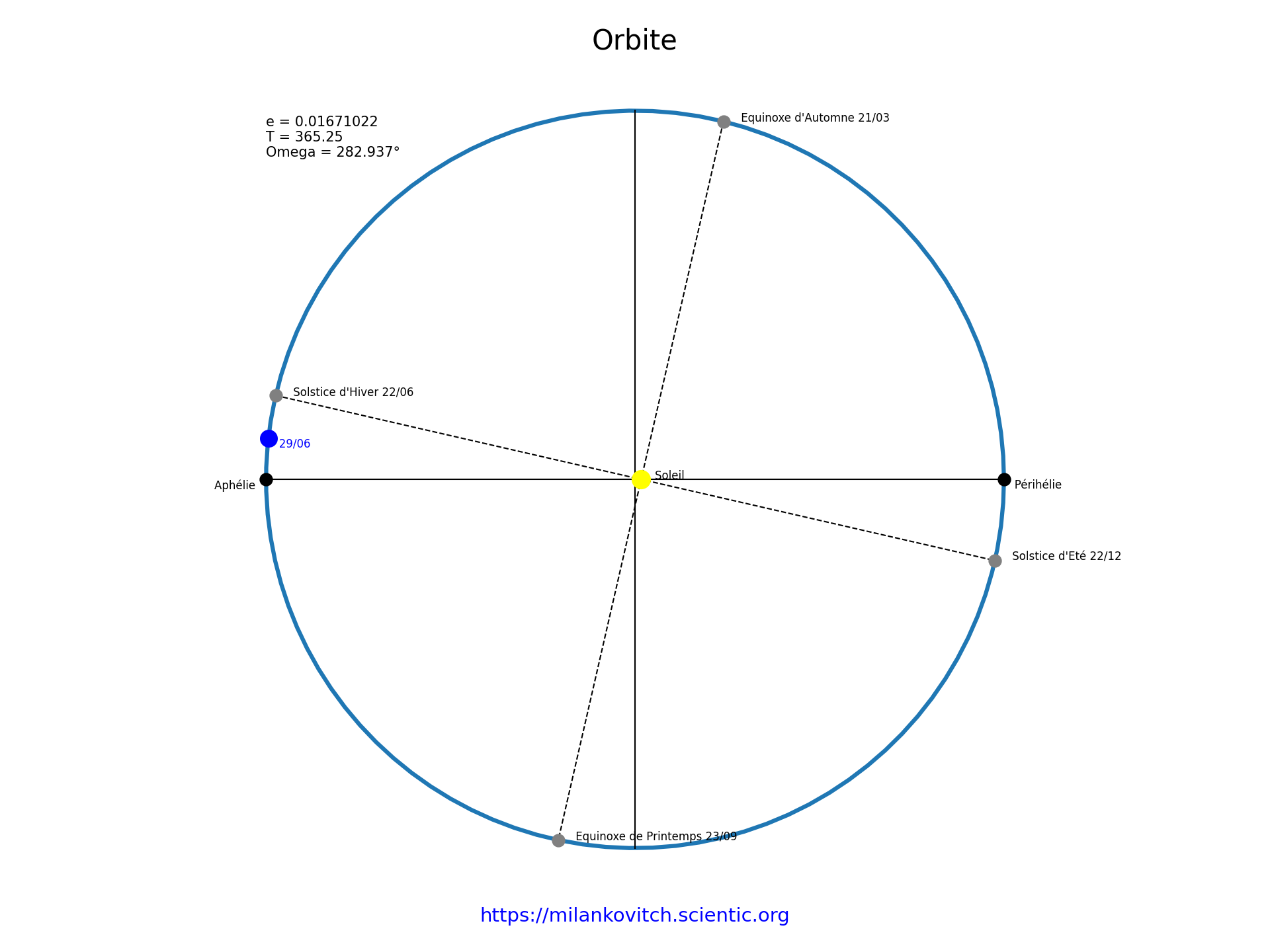
180° < ϖ < 360° |
 |
 |
 |
 |
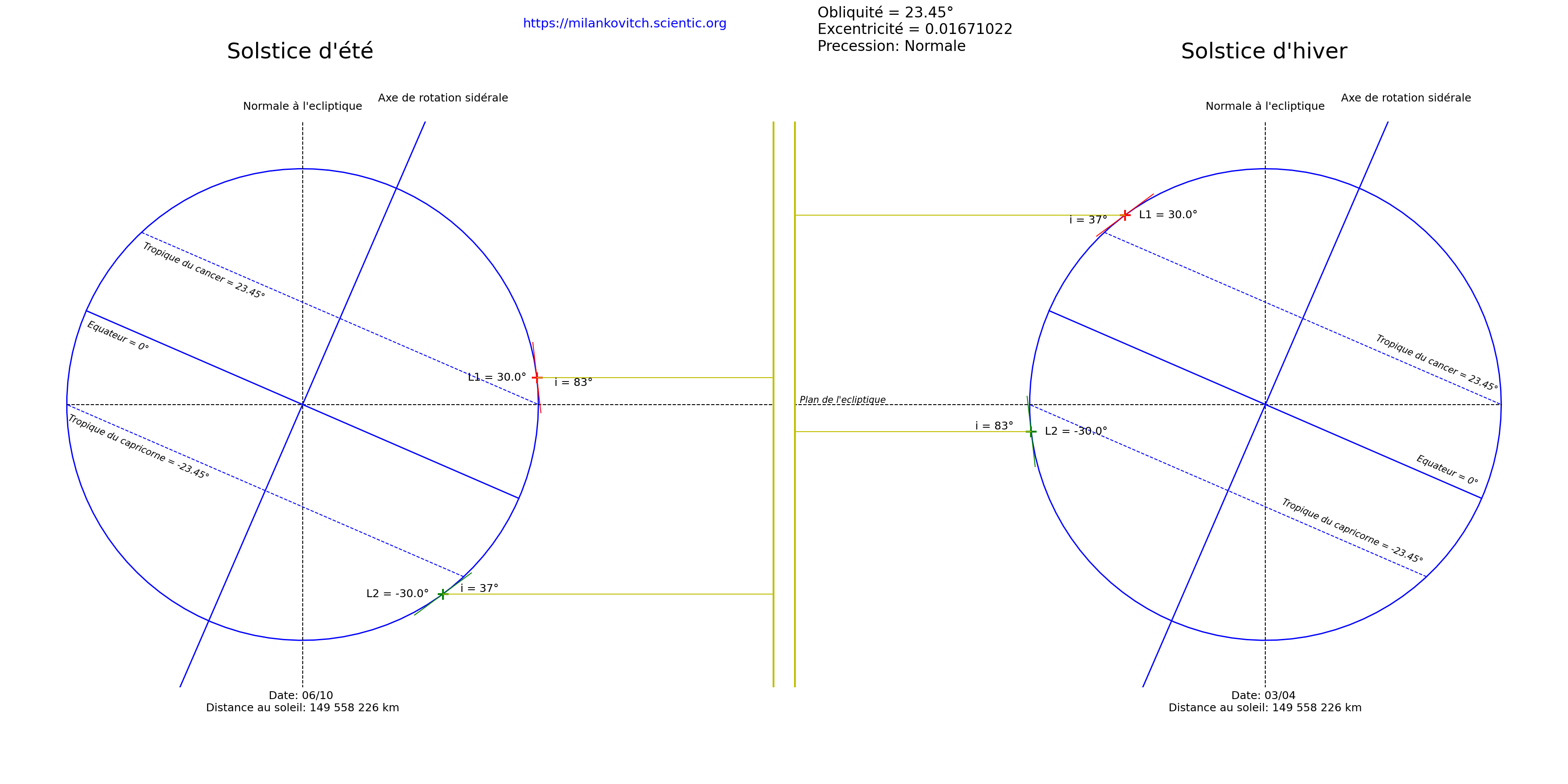 |
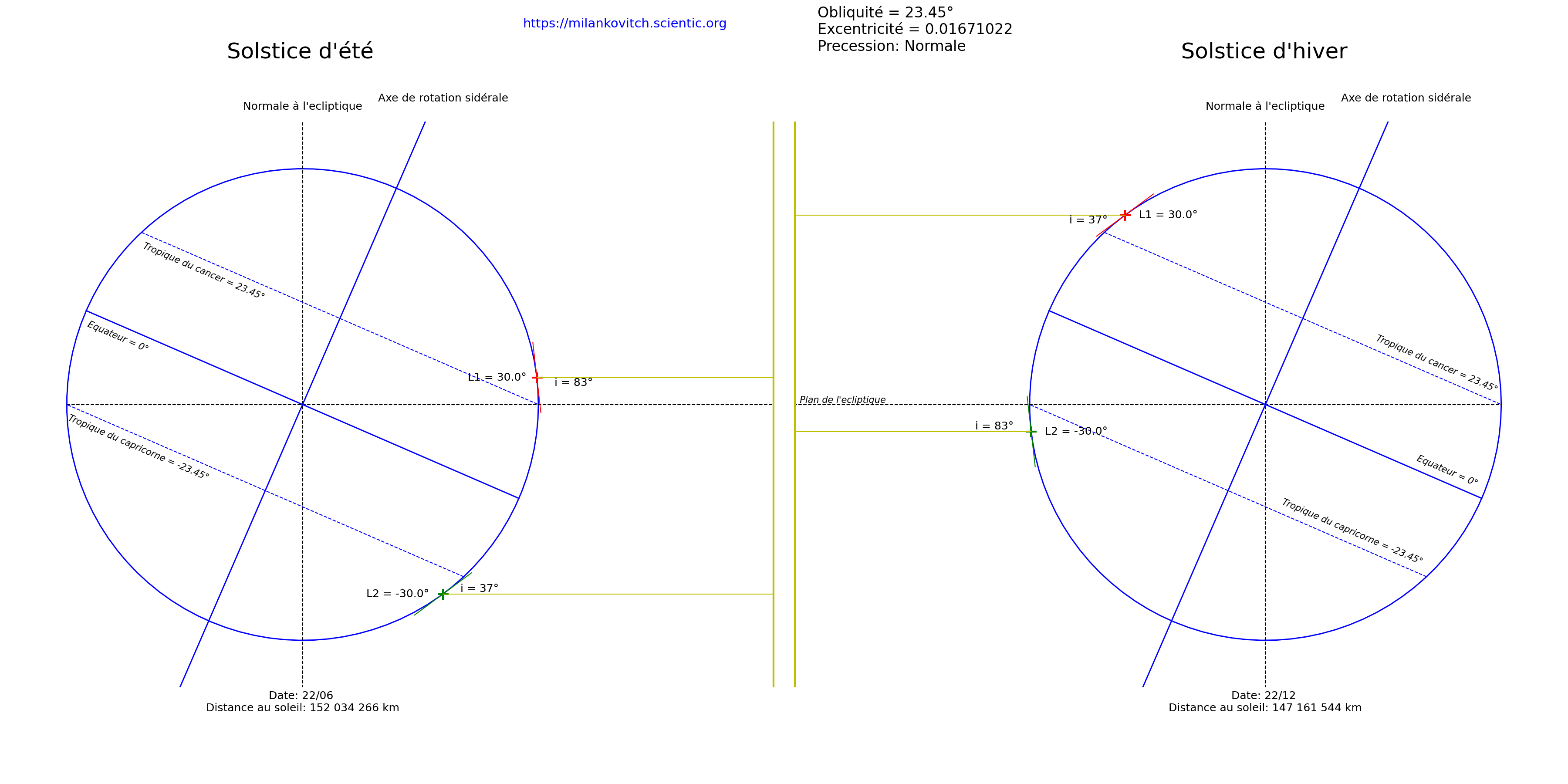 |
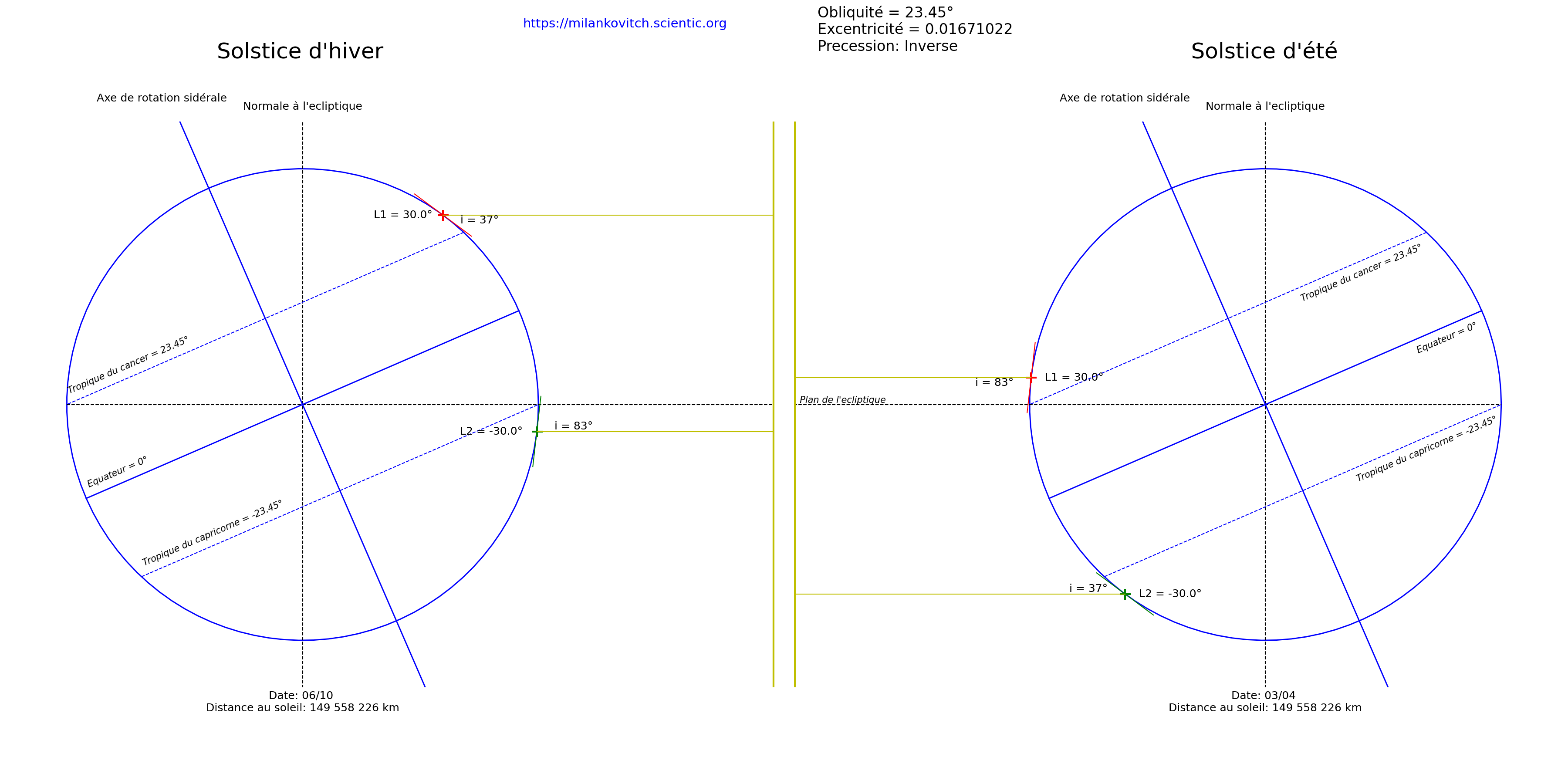 |
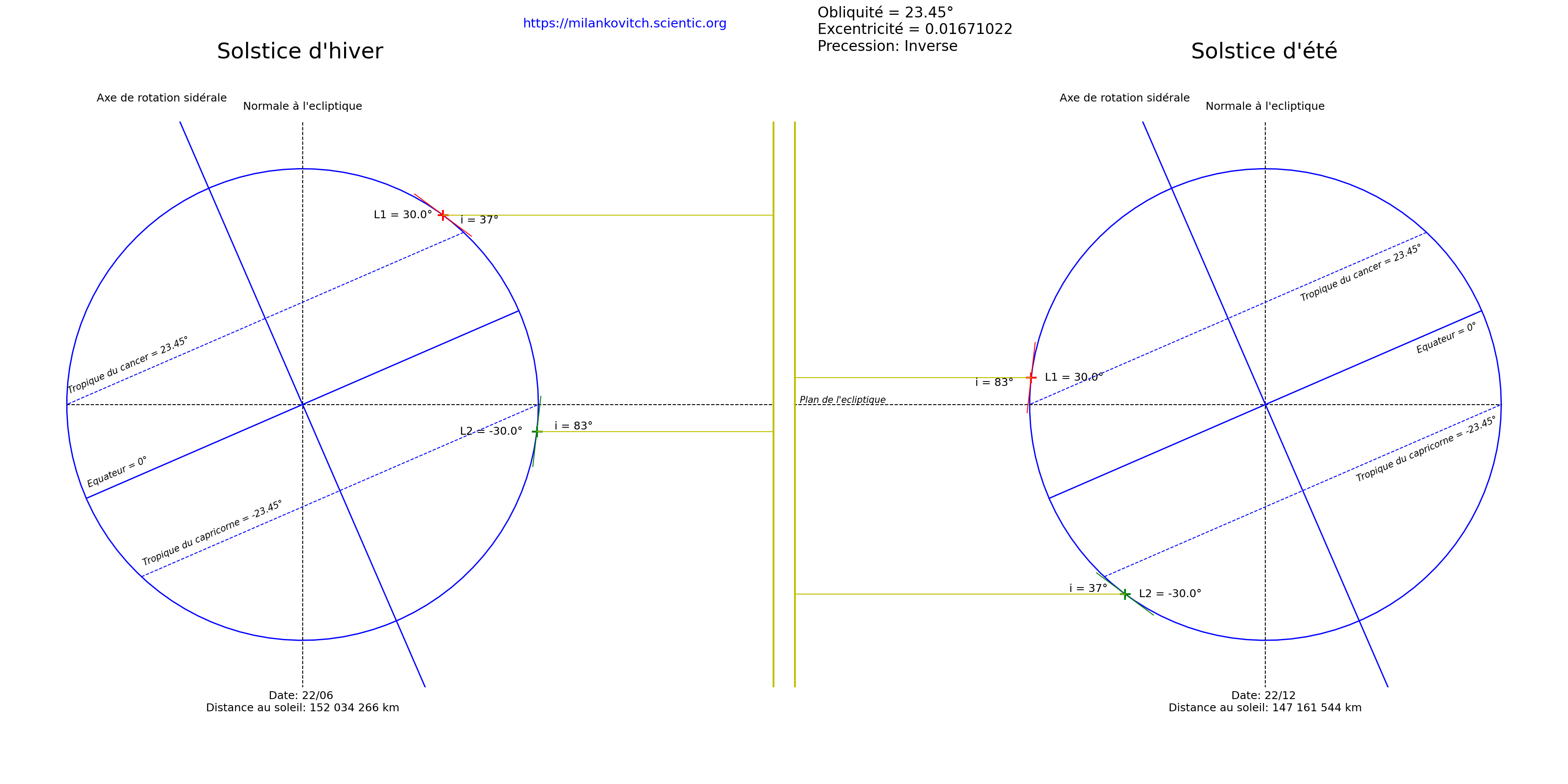 |
| Lorsque la longitude du périhélie ϖ est égale à 0°, la Terre est à la même distance du Soleil lors du solstice d’été et lors du solstice d’hiver.L'équinoxe de printemps coîncide avec l'aphélie, tandis que l'équinoxe d'automne coîncide avec le périhélie.La longitude du périhélie n’a pas d’incidence sur le contraste saisonnier qui ne dépend alors que de l’obliquité. |
Lorsque la longitude du périhélie ϖ est comprise entre 0° et 180°, comme c’est le cas actuellement (ϖ = 102,937°), la Terre est alors plus proche du Soleil lors du solstice d’hiver et plus loin du Soleil lors du solstice d’été.Il y’a donc moins de contrastes saisonniers dans l’hémisphère Nord (hivers moins froids - étés moins chauds), et davantage de contrastes saisonniers dans l’hémisphère Sud (hivers plus froids - étés plus chauds)Si ϖ = 90° alors le solstice d'été coîncide avec l'aphélie, tandis que le solstice d'hiver coîncide avec le périhélie. |
Lorsque la longitude du périhélie ϖ est égale à 180°, la Terre est à la même distance du Soleil lors du solstice d’été et lors du solstice d’hiver.L'équinoxe de printemps coîncide avec le périhélie, tandis que l'équinoxe d'automne coîncide avec l'aphélie.
La longitude du périhélie n’a pas d’incidence sur le contraste saisonnier qui ne dépend alors que de l’obliquité. |
Lorsque la longitude du périhélie ϖ est comprise entre 180° et 360°, comme c’est le cas dans une situation inverse à l’actuelle (ϖ = 282,937°), la Terre est alors plus loin du Soleil lors du solstice d’hiver et plus proche du Soleil lors du solstice d’été.Il y’a donc davantage de contrastes saisonniers dans l’hémisphère Nord (hivers plus froids - étés plus chauds), et moins de contrastes saisonniers dans l’hémisphère Sud (hivers moins froids - étés moins chauds)Si ϖ = 270° alors le solstice d'été coîncide avec le périhélie tandis que le solstice d'hiver coîncide avec l'aphélie. |